CV
☰
HOME RESEARCH

黄忠淦

Zhonggan Huang

ABOUT ME

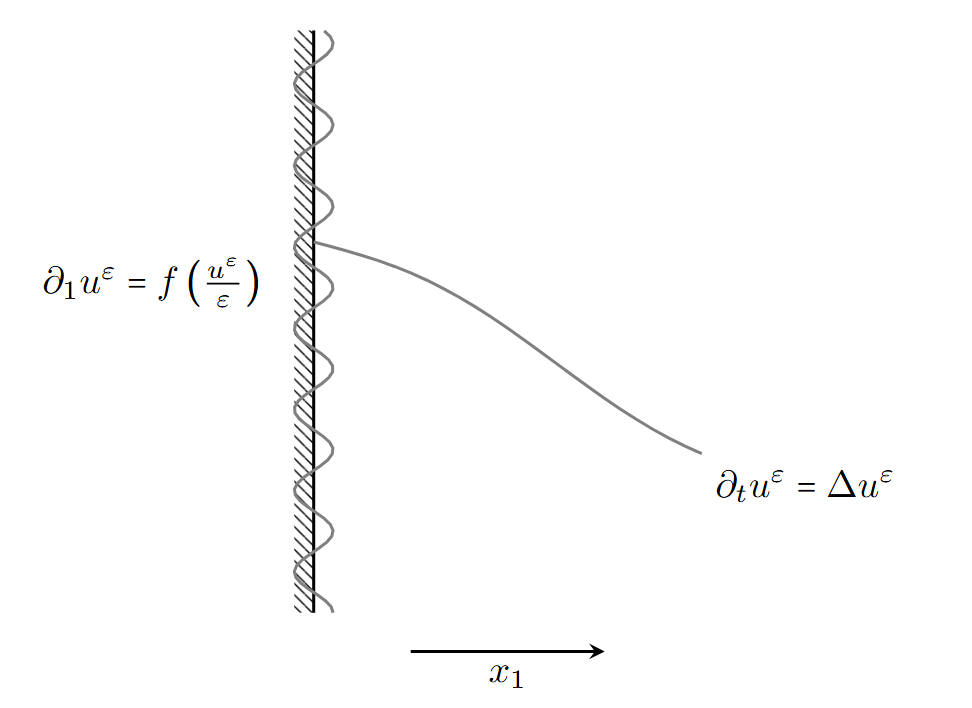
I am a 5th-year PhD student in the Department of Mathematics, University of Utah. My advisor is Prof. W. Feldman. I'm interested in homogenization theory, free boundary problems and shape optimization problems.

MY CONTACT DETAILS

Address: 155 South 1400 East, JWB 319, Department of Mathematics, University of Utah, Salt Lake City, U.S.

E-mail: zhonggan@math.utah.edu

EDUCATION

University of Utah, PhD in Mathematics

Aug 2021 – Jul 2026 (expected)

SUSTech, Master of Mathematics

Sep 2019 – Jun 2021

SUSTech, Bachelor of Mathematics

Sep 2015 – Jun 2019

溯洄从之，道阻且长。溯游从之，宛在水中央。

DOWNLOAD CV

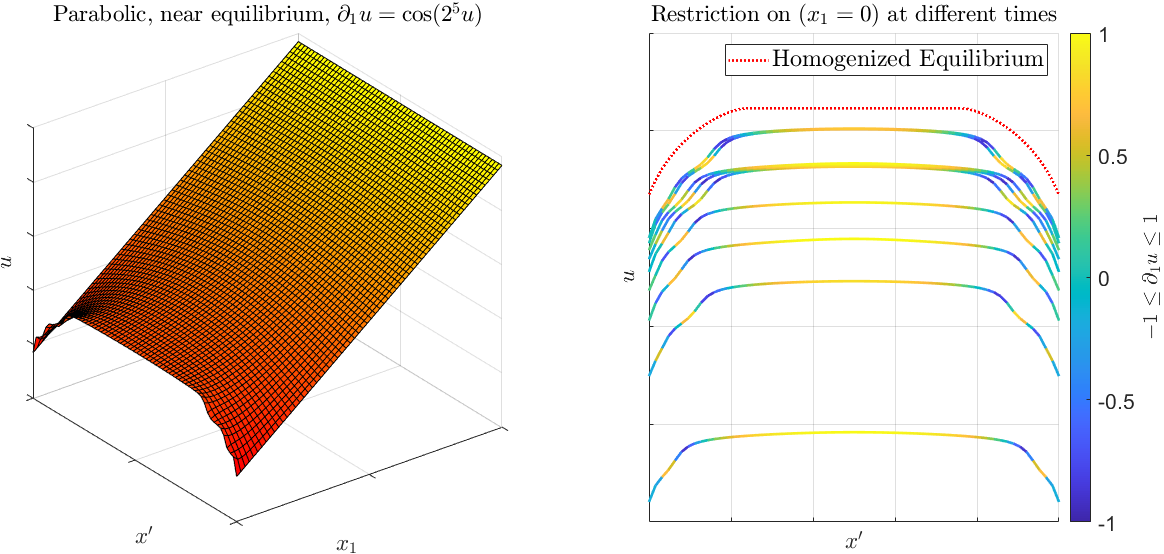
Recent figures

Leaf veins of Ampelocera ruizii
Reticulate \(\mathbb{Z}^2\)-periodic network (full rank)
Non-reticulate \(\mathbb{Z}^2\)-periodic network (zero effective tensor)
Non-reticulate \(\mathbb{Z}^2\)-periodic network (rank 1 effective tensor)
Maximal conductance \(\mathbb{Z}^2\)-periodic network (full rank)
Left: a picture of higher-order veins in a tropical forest tree, Ampelocera ruizii. The picture is reproduced from (Sack & Scoffoni, 2013), with permission from Wiley; Middle left: a reticulate \(\mathbb{Z}^2\)-periodic network that has full rank effective tensor; Middle: a non-reticulate \(\mathbb{Z}^2\)-periodic network that has zero effective tensor; Middle Right: a non-reticulate \(\mathbb{Z}^2\)-periodic network. It maximizes the effective conductance but the rank is 1. Right: a \(\mathbb{Z}^2\)-periodic network that maximizes the effective conductance and has full rank. It is also an irreducible periodic stationary network.
A graphical illustration of the PDE
midll
Left: A graphical illustration of the PDE to be homogenized; Middle: The small scale is \(\varepsilon=1/2^5\). The initial data is \(2x_1\) and the Dirichlet boundary condition is \(2x_1+2\tan^{-1}(t)\); Right: The graphs of the restriction of \(u^\varepsilon\) to the boundary \(\{x_1=0\,\}\) at integer times from 1 to 9. The colors represent the value of \(\partial_1 u\). One can observe that there are already hysteretic pinning phenomenon for positive \(\varepsilon\). I want to thank 许钊箐 (Zhaoqing Xu) for the help in generating the two figures on the right.